e (自然常数,也称为欧拉数)是自然对数函数的底数。它是数学中最重要的常数之一,是一个无理数,就是说跟 π 一样是无限不循环小数,在小数点后面无穷无尽,永不重复......
下面就是 e 的 2999 位有效数字,请注意不同的位我用不同的颜色表示出来了,有规律吗?还是随机的呢?

与我们更熟知的两个无理数圆周率 π 和 √2 不同,它不是由数学家由几何问题上发现而来的,而出自一个金融问题,是用来表示增长率和变化率的常数,很多增长与衰减过程中都出现了 e 的身影。
它为什么会和增长率有联系呢? 让我们回到来 17 世纪,看看发现 e 的第一人:瑞士数学家雅各布·伯努利以及他所研究的这个银行的利率问题.

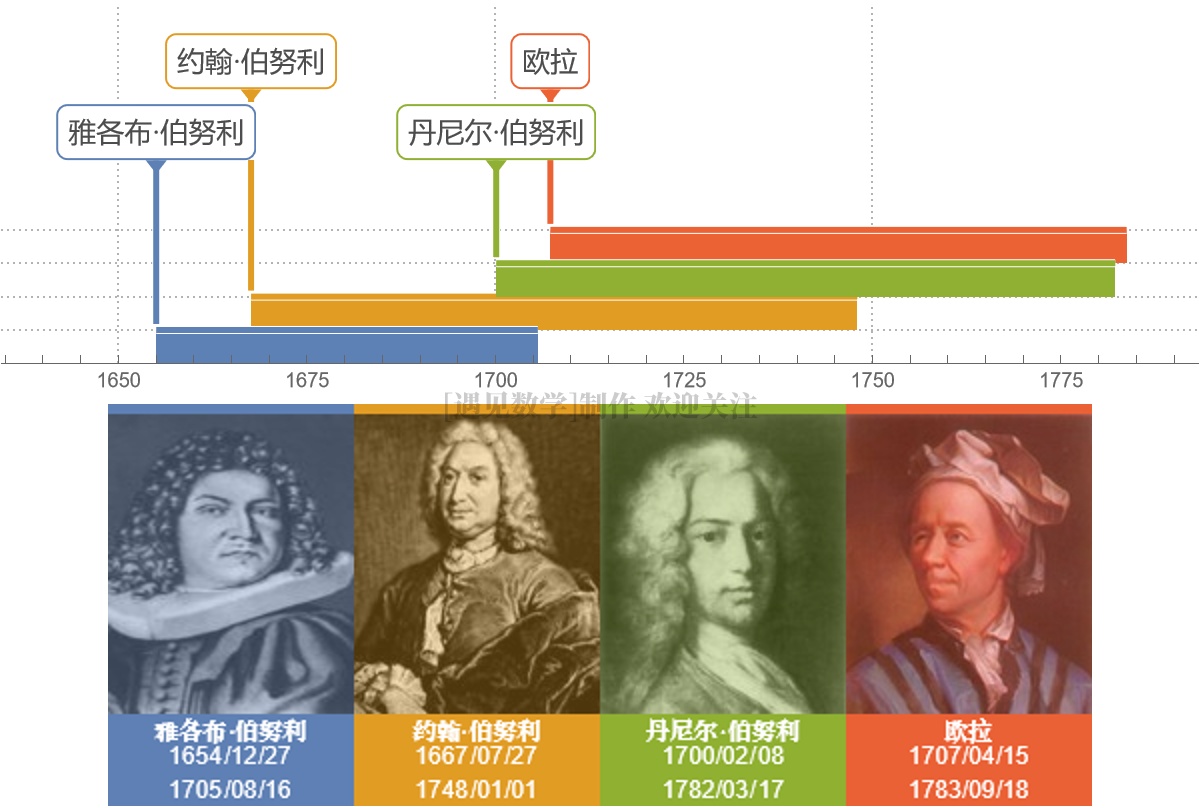
▲ 伯努利家族里的几位数学家与欧拉

e 与复利问题
雅各布·伯努利在研究复利的时候发现了一个有趣的现象: 假设在银行存了 1 块钱本金,而银行提供的年利率是 100%。这样的话,1 年后连本带息,将会得到 2 块钱,这个非常容易理解。
那么现在考虑改变计息的周期,假设半年就计算一次利息,半年利率为 50%,这样下半年新得到的利息同样可以生息。这样方案最终的收益应该比前一种更好,如何计算最终收益需要用到复利公式。

解释一下上面的复利公式:FV(Future Value)是指财富在未来的价值;PV(Present Value)是指现值,亦即指本金;i(interest)是指周期内的固定利率或固定回报率,n 则是累计的周期。现在直接导入公式中就能算出一年后收益。
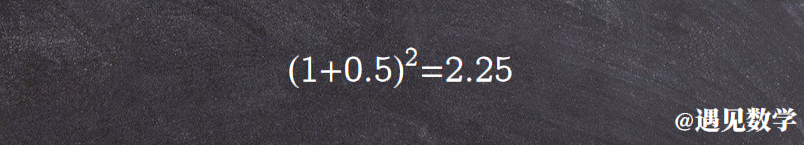
这样看来一年后共会获得 2.25 块钱。恩,看起来要比只计息一次强。那现在计算利率周期如果再短一些会怎么呢? 假设每个月结算一次呢?这样月利率为 1/12 ,上面复利公式只要稍作改动,最终计算得到大约 2.61304 块钱,这个方案会又好一些。
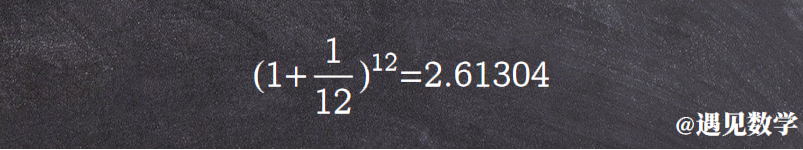
现在可以看出这样的规律,利息的周期越短,一年后的收益就更好. 那就让我们继续缩短计息的周期,变为每周计算,这样一年计息的次数就是 52 次 .
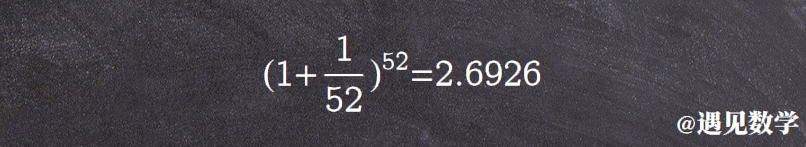
回报继续增加,这样我们甚至可以按每天来计息,或者半天、小时、分、秒来计算. 当然年末所获得的收益亦会继续增多. 不过雅各布.伯努利发现随着 n 趋于无穷,对于这样的连续复利存在着一个极限,一个神秘的数学常数由此出现了:
对于上面式子考虑的极限值将是多少呢?
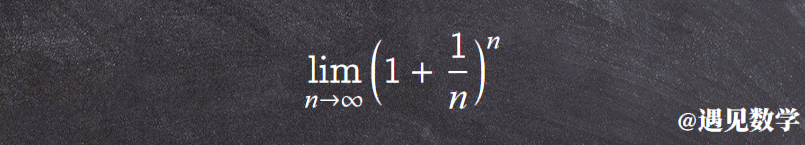
伯努利知道会是一个 2~3 之间的数,尝试许久。但最终很可惜他并没有计算出来. 这个问题由 50 年后,也就是1748年由瑞士数学家莱昂哈德·欧拉借助下面的公式计算出来 e 的小数点后 18 位
2.718281828459045235......,这就是描述增长率的自然常量 e 由来.
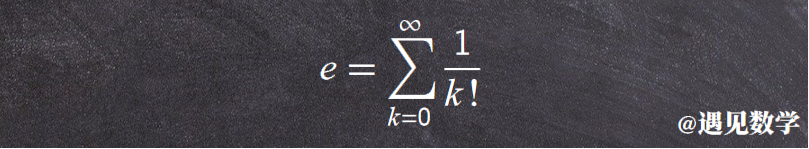
e 是无理数
欧拉不仅算出了 e 的 18 位数,并且还借助连分式的形式证明了 e 是一个无理数。下面图像是 e 小数点后 21 位的连分数形式,观察最左侧是 1,1,4,1,1,6,1,1,8,1,1,10,1,1,12……。

发现规律了没有?如果取得 e 小数点后无穷位的话,这样连分数展开式就满足这样有趣的模式,那就意味着它是个无理数.
欧拉恒等式中 e
既然提到了 e ,通常会提到将所有著名的常数出现在同一个方程 - 欧拉恒等式(Euler's identity),被美国物理学家费曼誉为最美的数学公式。因为这个等式居然把数学上 5 个最基本且重要的常数如此巧妙地联系起来。
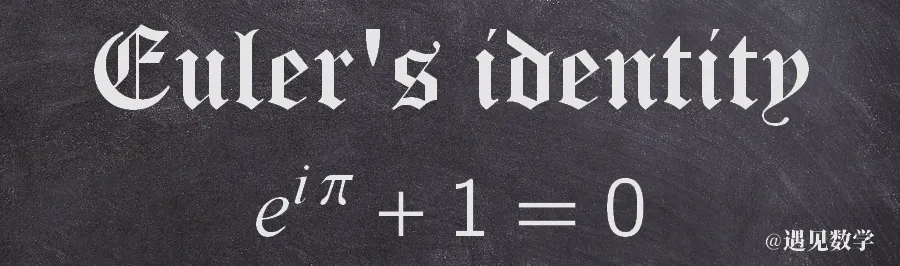
这个式子究竟是怎样出现的,我想就在另一篇文章中再介绍吧!

