在行测数量关系考试中,排列组合问题往往让考生感到困扰,因其题型多变,不少考生在考试中选择了放弃。但其实排列组合之中有一类难度较低的题型,我们将其称为错位重排。下面,MVP学习网就带领大家来了解一下考试中的错位重排是如何呈现的。
一、何为错位重排
错位重排又被称作装错信封问题,最早是伯努利和欧拉研究的。问题写道:“一个人写了n封不同的信及有n个相应的不同信封,问n封信全部装错信封的方法有多少种?”
二、错位重排的公式
粗略看来,如果n值较小,大家可以通过枚举进而得到答案,例如n=1时,没有错位重排;n=2时,错位重排数等于1;但随着n值的增大,通过枚举得出答案就愈发困难。所以对于这类问题有固定的递推公式,大家就要有所掌握:

三、错位重排的应用
【例1】将标有字母abcd的四个苹果放入标号为abcd的四个盒子中,但每盒只放一个,则每个盒子的标号与所放苹果的标号不相同的放法有多少种?( )
A.7 B.8 C.9 D.11
【答案】C。核心解析:每个苹果的字母和盒子的标号不一一对应,属于错位重排问题,且为4个元素。4个元素的错位重排记为D4=9。故本题选C。
【例2】某软件研发小组有5个开发人员,每人完成一个模块的开发后进行测试,每个人只负责测试一个模块,且不能测试自己开发的模块。问有几种不同的测试方案?( )
A.24 B.115 C.40 D.44
【答案】D。核心解析:每个人测试的模块和自己开发的模块不一一对应,属于错位重排问题,且为5个元素。5个元素的错位重排记为D5=44。故本题选D。
【例3】五个瓶子都贴了标签,其中恰好贴错了三个,贴错的可能情况有多少种?
A.6 B.10 C.12 D.20
【答案】D。核心解析:此题对比上述两题会发现有所变化,恰好贴错三个标签,说明还有两个标签贴对。第一步,先选出贴对的两个瓶子,也就是首先从5个瓶子中选出2个瓶子,即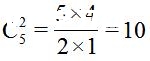 种;第二步将剩余3个标签贴错,即标签和瓶子都不一一对应,为3个元素的错位重排数D3=2。因此总情况数为分步相乘10*2=20。故本题选D。
种;第二步将剩余3个标签贴错,即标签和瓶子都不一一对应,为3个元素的错位重排数D3=2。因此总情况数为分步相乘10*2=20。故本题选D。
通过上面三道错位重排题目的学习,MVP学习网相信大家对错位重排这一解题方法有了一定的了解,大家一定要对排列组合问题中的错位重排问题多加练习,在考题中遇到此类问题也会迎刃而解!

