在做行测数量关系题目时经常会遇到一元二次函数,如求解、求极值等,其中考察求极值的题目相对会更多一些。虽然这是中学阶段学过的知识点,但不少同学们有所遗忘。那么接下来,MVP学习网就带着大家一起回顾一下一元二次函数求极值的三种常用方法,一起来看看吧!
一般地,把形如y=ax²+bx+c(a≠0)(a、b、c是常数)的函数叫做二次函数,其中a称为二次项系数,b为一次项系数,c为常数项。图象为左右对称的抛物线。

(1)当a>0时,抛物线开口向上,有最小值,图象如下:
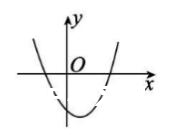

(2)当a<0时,抛物线开口向下,有最大值,图象如下:
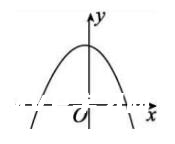

在求一元二次函数的极值时,有如下三种常用方法:
方法一:一般式。
y=ax²+bx+c(a≠0),一元二次函数在图象对称轴
方法二:交点式。
将一元二次函数整理为y=a(x-x1)(x-x2)的形式,在函数图象与x轴有两个交点的情况下,可先求出y=0时x的两个值x1和x2,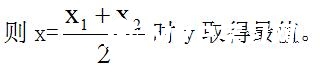
方法三:结合均值不等式。
将一元二次函数整理为y=a(m+x)(n-x)的形式。因(m+x)与(n-x)之和为定值,根据均值不等式原理,当且仅当m+x=n-x时,y取得最值。
接下来,我们通过一道题目进一步感受。
例.某电脑商城出售10种价格档位的电脑。最低价格档位的电脑每月可售出120台,每台可获利160元。每提升一个价格档位,则月销售量就会减少10台,但单台利润可增加40元。若某月该电脑商城只出售某一种价格档位的电脑,则当月可获得的最大利润是( )元。
A.24000 B.25600 C.27040 D.28000
【核心解析】B。方法一,设该月售出电脑的价格档位比最低价格档位高x个档位,则该月可售出(120-10x)台电脑,每台获利(160+40x)元。当月可获得的利润为(160+40x)×(120-10x)=-400x2+3200x+19200,当x=-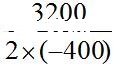 =4时获得的利润最多,最大利润为(160+40×4)×(120-10×4)=320×80=25600元。故本题选B。
=4时获得的利润最多,最大利润为(160+40×4)×(120-10×4)=320×80=25600元。故本题选B。
方法二,设该月售出电脑的价格档位比最低价格档位高x个档位,则该月可售出(120-10x)台电脑,每台获利(160+40x)元。当月可获得的利润为(160+40x)×(120-10x)=400(4+x)×(12-x)。当400(4+x)×(12-x)=0时,x为-4或12,则当x=(-4+12)÷2=4时,获得的利润最多,最大利润为(160+40×4)×(120-10×4)=320×80=25600元。故本题选B。
方法三,设该月售出电脑的价格档位比最低价格档位高x个档位,则该月可售出(120-10x)台电脑,每台获利(160+40x)元。当月可获得的利润为(160+40x)×(120-10x)=400(4+x)×(12-x)。根据均值不等式原理,当且仅当4+x=12-x,即x=4时,获得的利润最多,最大利润为(160+40×4)×(120-10×4)=320×80=25600元。故本题选B。
MVP学习网希望通过以上题目的交流,能让各位同学基本掌握一元二次函数求极值的三种常用方法。大家可以在备考中多多练习该种类型的题目,以熟练掌握解题方法。

