每年高考数学,江苏卷和浙江卷都是全国各类型高考题中较难的试卷。相比之下,他们的计算量更大,考察角度更灵活多变。所以也是众多考生考后喜欢议论的话题。尤其是江苏卷试卷比较新颖,和其他区域考试试卷不同,他取消了选择题部分,取而代之的是增加了填空题的数量。笔者之前已经对江苏卷的填空题部分进行了解析,今天就给大家详细解析下大题部分,看看2023年高考江苏卷数学难度究竟如何,这里面重点考察我们哪方面的知识,同时又有怎样的解题技巧值得学习借鉴。



15题,典型的三角函数题型,难度不是很大,重点考察我们正弦定理以及余弦定理的运用。只要掌握相应的公式,那么进行简单的变形便能得出最终答案。



16题,简单的立体几何题型。在今年所有区域的立体几何题中,江苏卷的立体几何算是最简单的了,几乎没怎么转弯,也没有必要建立空间直角坐标系,利用一些基础概念定理,便能得出结论。


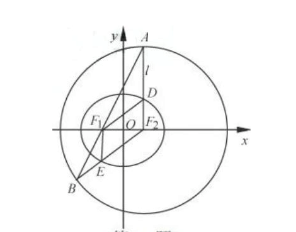

17题,圆锥曲线题型。这个题的突破口在于分析清楚图中各线段之间的关系,结合椭圆的性质定理,第一问就很容易求解。第二问从表面上看需要我们求很多点的坐标,但是由于已知点的坐标较多,求解也很方便。总体思路是多次利用直线与圆或直线与椭圆的方程求解出对应点的坐标,难度不算很大。


18题,三角函数及圆的一些基础知识考察。第一问比较简单,结合题意添加一条辅助线AE垂直于BD,那么四边形AEDC便能得证是矩形,确定AE、BE的长度,接下来求解就很方便了。第二问的求解始终围绕一个知识点,那就是:当直线与与圆相切时,直线上的点到圆心的距离不小于半径。换成角度来表达便是直线与半径所构成的角要大于等于90°才能满足题意。那么结合这一点,我们便能进行求解了。


19题,函数题型,第一问结合已知条件很容易就能求出,第二问首先找出f(x)与其倒数零点的表达式,再结合已知条件求出a、b的值,然后利用倒数求出f(x)的单调区间,找出极小值。第三问思路有些类似,同样是利用倒数找出单调区间再写出极大值的表达式,最后对极大值的表达式进行化简,推出其小于等于4/27。


20题,数列题,这道题的难度会大一些。第一问根据题干条件很容易求出首项和公比,然后证明结论。第二问第一小问的突破口在于求出Sn的表达式,然后结合bn=Sn-Sn-1这一性质表示出bn,将最终表达式化解后便能得出一个明显的等差数列的等差中项的表达式,便能说明bn是等差数列,然后根据首相和公差,便能写出通项公式。
而第二小问难度较大,其突破口在于将指数不等式转换为对数不等式,然后构建Lnx/x的新函数,利用倒数判断出函数的单调性,找出极大值,接下来便是对k的取值进行讨论,根据最初题干给出的不等式进行验证,最终得出m的最大值。


21题,作为选做题分为三个部分,都不是很难。A题,矩阵乘法的运算及特征值的求法,只要知道运算规则,那么这个题很快就能求出答案。
B题,极坐标的相关知识。这儿首先要大家理解极坐标表达式的意义,明确起每个坐标代表的含义,然后结合图形,便能快速求解。此外要掌握直线方程或圆锥曲线方程与极坐标方程之间的转换方法。
C题,简单的分段讨论不等式题型,对x的取值范围进行分情况讨论,得出几个范围,最终合并即可。


22题,二项式定理的考察,总体难度不高,只要熟悉二项式定理公式,那么这道理无非就是简单的计算而已。没多大难度。



23题,概率题型。在求解这道题之前要明白这道题表达的意思。绘制出草图,利用简单勾股定理的知识表示出两点间的距离。尤其是第二问,要针对两个点的不同位置进行分情况讨论,最终才能得出正确答案。总的来说难度不是很大,只是过程会比较繁琐,需要更多的耐心。
总的来看,2023年高考江苏卷数学难度中上,相对而言数列题、函数题和概率题有一定的难度。其他题只要基础扎实,应该问题不大。不知道屏幕前的诸位都发挥得如何呢?

